


|
 |

#1  barboZz @ 14.01.11 21:51
barboZz @ 14.01.11 21:51 |
[пожаловаться]
|
 |
1/(1+x^6) найти 300 производную
хотя бы нужна идея.
если искать закономерность, то её тут нет)
thx заранее
хэлпа потсоны
зы не голоден.
зы зы
|
|
 |
#5  barboZz @ 14.01.11 22:02
barboZz @ 14.01.11 22:02 |
[пожаловаться]
|
 |
ну как бы нашел первую, вторую, третью, закономерности никакой О_О
так что х7л3 тут
подсобите
|
|
 |
#6  gilbert @ 14.01.11 22:03
gilbert @ 14.01.11 22:03 |
[пожаловаться]
|
 |
покажи первые 3 производные
ps. на заводе тебе это не пригодится
|
|
 |
#9  leniva @ 14.01.11 22:09
leniva @ 14.01.11 22:09 |
[пожаловаться]
|
 |
3647b автор я уже и забыл какую страшную куйню вы изучаете в школе 
ЗЫ решебник в помосчь
|
|
 |
#12  figishman666 @ 14.01.11 22:12
figishman666 @ 14.01.11 22:12 |
[пожаловаться]
|
 |
блеать,аффтор есть же формула Лейбница нахождения n-ой производной.гугли!
|
|
 |
#13  barboZz @ 14.01.11 22:12
barboZz @ 14.01.11 22:12 |
[пожаловаться]
|
 |
1ая: -6x^5/(1+x^6)^2
2я: (72x^10 - 30x^4)/(1+x^6)^3
3я: ( (720x^9 - 120x^3)(1+x^6)^3 - 18x^5(72x^10 - 30x^4)(1+x^6)^2 ) / (1+x^6)^6
O_O
|
|
 |
#15  leniva @ 14.01.11 22:13
leniva @ 14.01.11 22:13 |
[пожаловаться]
|
 |
№13 разгадал формулу адронного калайдера 
ЗЫ если завтра земля взорвется , я на тебя в прокуратуру напишу
|
|
 |
#16  ч0ткость_сэр @ 14.01.11 22:15
ч0ткость_сэр @ 14.01.11 22:15 |
[пожаловаться]
|
 |
Формула Лейбница для n-ой производной произведения двух функций — обобщение правила дифференцирования произведения (и отношения) двух функций на случай n-кратного дифференцирования.
Пусть функции f(z) и g(z) — n раз дифференцируемые функции, тогда
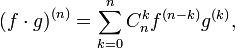 где — б где — б 
|
|
 |
#17  figishman666 @ 14.01.11 22:15
figishman666 @ 14.01.11 22:15 |
[пожаловаться]
|
 |
и как это блеать нет закономерности?!степень икса знаменателя все время увиличивается 7,8,9...,а множитель числителя увиличивается так 6,6*7,6*7*8,6*7*8*9...
|
|
 |
#20  barboZz @ 14.01.11 22:22
barboZz @ 14.01.11 22:22 |
[пожаловаться]
|
 |
#16 так, число сочетаний из n по к
n=300
а чему равно k?
и если разбить 1/1+x^6 на f и g то типа f=1 а g= (1+x^6)^-1
но прозводная 1 всегда 0
тем самым них7я не получается
т.е чото тут
|
|
 |
#21  ч0ткость_сэр @ 14.01.11 22:24
ч0ткость_сэр @ 14.01.11 22:24 |
[пожаловаться]
|
 |
k-число от нуля до n, необязательно разбивать так, разбей так:
f=x g=1/x(1+x^6)
|
|
 |
#22  barboZz @ 14.01.11 22:24
barboZz @ 14.01.11 22:24 |
[пожаловаться]
|
 |
#17
покажи конкретнее где и что увеличивается? О_О
особенно в 3ей производной мне очень интересно))
|
|
 |
#23  barboZz @ 14.01.11 22:27
barboZz @ 14.01.11 22:27 |
[пожаловаться]
|
 |
#21 кэп
но
нам нужно конкретное число сочетаний
конкретное k, а n=300
и чо толку , что f=x ? O_O
вторая производная x-а равна 0.
и всё
|
|
 |
#24  figishman666 @ 14.01.11 22:28
figishman666 @ 14.01.11 22:28 |
[пожаловаться]
|
 |
аффтар ну ты и тормоз!n-это то количество производных,которые ты собираешься взять.k-это шаги-1,2,3...300.и каким таким образом ты разбил одну функцию на две?это ж не произведение.бери производную от (1+х^6)^(-1). а главное не забывай про свойство-произведение внешней умножается на произведение внутренней. где внешняя это исходная,а внутренняя это 1+x^6. удачи
|
|
 |
#26  ч0ткость_сэр @ 14.01.11 22:30
ч0ткость_сэр @ 14.01.11 22:30 |
[пожаловаться]
|
 |
парень, ты не понял, на значок суммы обрати внимание, пожалуйста, то что вторая производная равна 0 лишь обнуляет один из 300 других членов суммы, почему тебя это смущает?
|
|
 |
#28  barboZz @ 14.01.11 22:33
barboZz @ 14.01.11 22:33 |
[пожаловаться]
|
 |
#26
парень
посмотри на формулу
в ней произведение двух функций f и g. n-я производная
т.е мою функцию надо разложить на 2
(f*g)^(n) = (1*(1+x^6)^-1 )^ (300)
а если k - кол-во шагов. то сколько шагов мне делать и на каком шаге останавливаться О_О
|
|
 |
#29  barboZz @ 14.01.11 22:34
barboZz @ 14.01.11 22:34 |
[пожаловаться]
|
 |
#24
кэп
посмотри на формулу
в ней произведение двух функций f и g. n-я производная
т.е мою функцию надо разложить на 2
(f*g)^(n) = (1*(1+x^6)^-1 )^ (300)
а если k - кол-во шагов. то сколько шагов мне делать и на каком шаге останавливаться О_О
|
|
 |
#30  ч0ткость_сэр @ 14.01.11 22:36
ч0ткость_сэр @ 14.01.11 22:36 |
[пожаловаться]
|
 |
парень, тебе не нужно делать шаги, все твои шаги записаны в значении суммы, разбиваешь (f*g)^(n) = (x/x(1+x^6)^-1 )^ (300)
|
|
 |
#34  barboZz @ 14.01.11 22:40
barboZz @ 14.01.11 22:40 |
[пожаловаться]
|
 |
#30
с7777777777к:AAAAAAAA 
напиши пожалуйста конкретно первые 2-3 шага
и сколько всего этиъ шагов?
|
|
 |
#35  figishman666 @ 14.01.11 22:46
figishman666 @ 14.01.11 22:46 |
[пожаловаться]
|
 |
пока k не станет равным n
а вообще она зануляться не должна,так как геометрически 1/(1+x^6) от 1/x^6 отличается лишь тем, что первая, в отличии от второй, на один смещенна вверх по оси у.а вторая диффиринцируется бесконечно много раз
|
|
 |
#37  barboZz @ 14.01.11 22:50
barboZz @ 14.01.11 22:50 |
[пожаловаться]
|
 |
300 шагов
мм
как мило
это точно не так делается
допустим 50-ый шаг
f^(n-k) = f^250 производная. кул стори
короче надо чето решать, потсоны...
|
|
 |
#40  a_ti_kto @ 14.01.11 22:58
a_ti_kto @ 14.01.11 22:58 |
[пожаловаться]
|
 |
20го матан сдавать
очково
из этого ниче не понял.
удачи мне.
халява прийди.
|
|
 |
#42  a_ti_kto @ 14.01.11 23:01
a_ti_kto @ 14.01.11 23:01 |
[пожаловаться]
|
 |
#41 удачи.
сдашь чей.
у тя препод наверняка адекватный, не как у меня.
это отдельная кул стори.
|
|
 |
#43  figishman666 @ 14.01.11 23:02
figishman666 @ 14.01.11 23:02 |
[пожаловаться]
|
 |
1ая: -(1+x^6)^(-2)*(6x^5)
2ая: 2*(1+x^6)^(-3)*(6x^5)-(1+x^6)^(-2)*30x^4
3я: -6*(1+x^6)^(-4)*(6x^5)+2*(1+x^6)^(-3)*30x^4+2*(1+x^6)^(-3)*(6x^5)-(1+x^6)^(-2)*120x^3
как-то так
|
|
 |
#46  barboZz @ 14.01.11 23:06
barboZz @ 14.01.11 23:06 |
[пожаловаться]
|
 |
#42
сэнкс
да хз
надо как то чето сдавать
#43
ты можешь представить что в трехсотой будет? О_О
мне кажется там странички не хватит чтоб записать
|
|
 |
#47  bro O_O @ 14.01.11 23:10
bro O_O @ 14.01.11 23:10 |
[пожаловаться]
|
 |
Превышена частота размещения сообщений - подождите несколько секунд.

|
|
 |
| Reply |  | |  |
|
 |
|









